UsdGeomBasisCurves#

Fully qualified name: usdrt::UsdGeomBasisCurves

class UsdGeomBasisCurves : public usdrt::UsdGeomCurves #

BasisCurves are a batched curve representation analogous to the classic RIB definition via Basis and Curves statements. BasisCurves are often used to render dense aggregate geometry like hair or grass.

A ‘matrix’ and ‘vstep’ associated with the basis are used to interpolate the vertices of a cubic BasisCurves. (The basis attribute is unused for linear BasisCurves.)

A single prim may have many curves whose count is determined implicitly by the length of the curveVertexCounts vector. Each individual curve is composed of one or more segments. Each segment is defined by four vertices for cubic curves and two vertices for linear curves. See the next section for more information on how to map curve vertex counts to segment counts.

Segment Indexing#

Interpolating a curve requires knowing how to decompose it into its individual segments.

The segments of a cubic curve are determined by the vertex count, the wrap (periodicity), and the vstep of the basis. For linear curves, the basis token is ignored and only the vertex count and wrap are needed.

cubic basis	vstep
bezier	3
catmullRom	1
bspline	1

The first segment of a cubic (nonperiodic) curve is always defined by its first four points. The vstep is the increment used to determine what vertex indices define the next segment. For a two segment (nonperiodic) bspline basis curve (vstep = 1), the first segment will be defined by interpolating vertices [0, 1, 2, 3] and the second segment will be defined by [1, 2, 3, 4]. For a two segment bezier basis curve (vstep = 3), the first segment will be defined by interpolating vertices [0, 1, 2, 3] and the second segment will be defined by [3, 4, 5, 6]. If the vstep is not one, then you must take special care to make sure that the number of cvs properly divides by your vstep. (The indices described are relative to the initial vertex index for a batched curve.)

For periodic curves, at least one of the curve’s initial vertices are repeated to close the curve. For cubic curves, the number of vertices repeated is ‘4 - vstep’. For linear curves, only one vertex is repeated to close the loop.

Pinned curves are a special case of nonperiodic curves that only affects the behavior of cubic Bspline and Catmull-Rom curves. To evaluate or render pinned curves, a client must effectively add ‘phantom points’ at the beginning and end of every curve in a batch. These phantom points are injected to ensure that the interpolated curve begins at P[0] and ends at P[n-1].

For a curve with initial point P[0] and last point P[n-1], the phantom points are defined as. P[-1] = 2 * P[0] - P[1] P[n] = 2 * P[n-1] - P[n-2]

Pinned cubic curves will (usually) have to be unpacked into the standard nonperiodic representation before rendering. This unpacking can add some additional overhead. However, using pinned curves reduces the amount of data recorded in a scene and (more importantly) better records the authors’ intent for interchange.

Linear curve segments are defined by two vertices. A two segment linear curve’s first segment would be defined by interpolating vertices [0, 1]. The second segment would be defined by vertices [1, 2]. (Again, for a batched curve, indices are relative to the initial vertex index.)

When validating curve topology, each renderable entry in the curveVertexCounts vector must pass this check.

type	wrap	validitity
linear	nonperiodic	curveVertexCounts[i] > 2
linear	periodic	curveVertexCounts[i] > 3
cubic	nonperiodic	(curveVertexCounts[i] - 4) % vstep == 0
cubic	periodic	(curveVertexCounts[i]) % vstep == 0
cubic	pinned (catmullRom/bspline)	(curveVertexCounts[i] - 2) >= 0

Cubic Vertex Interpolation#

../_images/USDCurveBasisMatrix.png

Linear Vertex Interpolation#

Linear interpolation is always used on curves of type linear. ‘t’ with domain [0, 1], the curve is defined by the equation P0 * (1-t) + P1 * t. t at 0 describes the first point and t at 1 describes the end point.

Primvar Interpolation#

For cubic curves, primvar data can be either interpolated cubically between vertices or linearly across segments. The corresponding token for cubic interpolation is ‘vertex’ and for linear interpolation is ‘varying’. Per vertex data should be the same size as the number of vertices in your curve. Segment varying data is dependent on the wrap (periodicity) and number of segments in your curve. For linear curves, varying and vertex data would be interpolated the same way. By convention varying is the preferred interpolation because of the association of varying with linear interpolation.

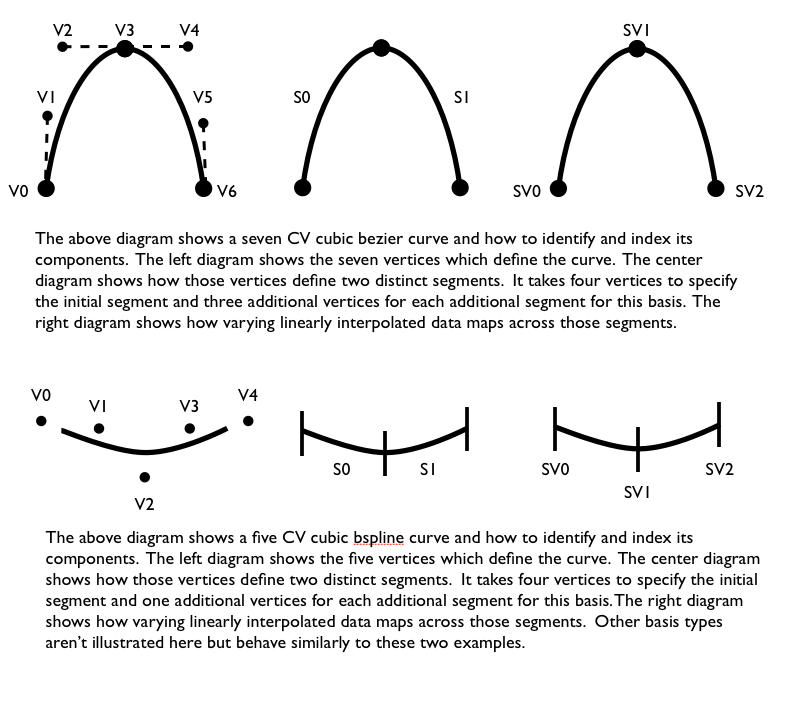
../_images/USDCurvePrimvars.png

To convert an entry in the curveVertexCounts vector into a segment count for an individual curve, apply these rules. Sum up all the results in order to compute how many total segments all curves have.

The following tables describe the expected segment count for the ‘i’th curve in a curve batch as well as the entire batch. Python syntax like ‘[:]’ (to describe all members of an array) and ‘len(…)’ (to describe the length of an array) are used.

type	wrap	curve segment count	batch segment count
linear	nonperiodic	curveVertexCounts[i] - 1	sum(curveVertexCounts[:]) -

The following table descrives the expected size of varying (linearly interpolated) data, derived from the segment counts computed above.

wrap	curve varying count	batch varying count
nonperiodic/pinned	segmentCounts[i] + 1	sum(segmentCounts[:]) + len(curveVertexCounts)
periodic	segmentCounts[i]	sum(segmentCounts[:])

Both curve types additionally define ‘constant’ interpolation for the entire prim and ‘uniform’ interpolation as per curve data.

As an example of deriving per curve segment and varying primvar data counts from the wrap, type, basis, and curveVertexCount, the following table is provided.

wrap	type	basis	curveVertexCount	curveSegmentCount	varyingDataCount
nonperiodic	linear	N/A	[2 3 2 5]	[1 2 1 4]	[2 3 2 5]
nonperiodic	cubic	bezier	[4 7 10 4 7]	[1 2 3 1 2]	[2 3 4 2 3]
nonperiodic	cubic	bspline	[5 4 6 7]	[2 1 3 4]	[3 2 4 5]
periodic	cubic	bezier	[6 9 6]	[2 3 2]	[2 3 2]
periodic	linear	N/A	[3 7]	[3 7]	[3 7]

Tubes and Ribbons#

The strictest definition of a curve as an infinitely thin wire is not particularly useful for describing production scenes. The additional widths and normals attributes can be used to describe cylindrical tubes and or flat oriented ribbons.

Curves with only widths defined are imaged as tubes with radius ‘width / 2’. Curves with both widths and normals are imaged as ribbons oriented in the direction of the interpolated normal vectors.

While not technically UsdGeomPrimvars, widths and normals also have interpolation metadata. It’s common for authored widths to have constant, varying, or vertex interpolation (see UsdGeomCurves::GetWidthsInterpolation()). It’s common for authored normals to have varying interpolation (see UsdGeomPointBased::GetNormalsInterpolation()).

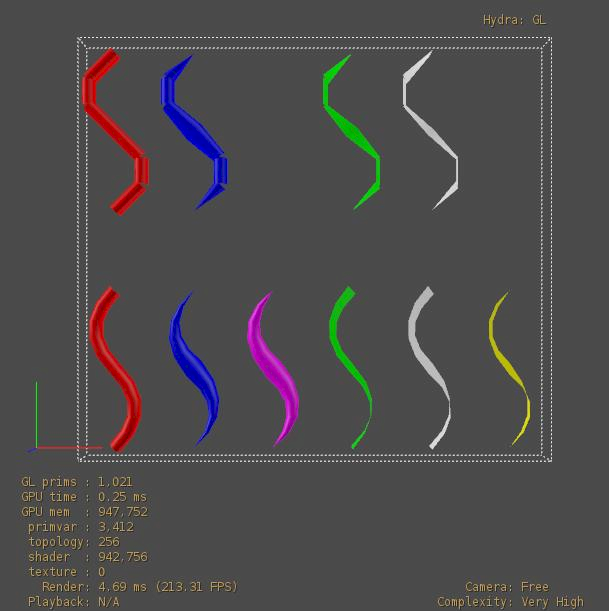
../_images/USDCurveHydra.png

The file used to generate these curves can be found in pxr/extras/examples/usdGeomExamples/basisCurves.usda. It’s provided as a reference on how to properly image both tubes and ribbons. The first row of curves are linear; the second are cubic bezier. (We aim in future releases of HdSt to fix the discontinuity seen with broken tangents to better match offline renderers like RenderMan.) The yellow and violet cubic curves represent cubic vertex width interpolation for which there is no equivalent for linear curves.

For any described attribute Fallback Value or Allowed Values below that are text/tokens, the actual token is published and defined in UsdGeomTokens. So to set an attribute to the value “rightHanded”, use UsdGeomTokens->rightHanded as the value.

Note

The additional phantom points mean that the minimum curve vertex count for cubic bspline and catmullRom curves is 2.

Note

Take care when providing support for linearly interpolated data for cubic curves. Its shape doesn’t provide a one to one mapping with either the number of curves (like ‘uniform’) or the number of vertices (like ‘vertex’) and so it is often overlooked. This is the only primitive in UsdGeom (as of this writing) where this is true. For meshes, while they use different interpolation methods, ‘varying’ and ‘vertex’ are both specified per point. It’s common to assume that curves follow a similar pattern and build in structures and language for per primitive, per element, and per point data only to come upon these arrays that don’t quite fit into either of those categories. It is also common to conflate ‘varying’ with being per segment data and use the segmentCount rules table instead of its neighboring varying data table rules. We suspect that this is because for the common case of nonperiodic cubic curves, both the provided segment count and varying data size formula end with ‘+ 1’. While debugging, users may look at the double ‘+ 1’ as a mistake and try to remove it. We take this time to enumerate these issues because we’ve fallen into them before and hope that we save others time in their own implementations.

Note

How did this prim type get its name? This prim is a portmanteau of two different statements in the original RenderMan specification: ‘Basis’ and ‘Curves’.

Public Functions

inline explicit UsdGeomBasisCurves(const UsdPrim &prim = UsdPrim())#: Construct a UsdGeomBasisCurves on UsdPrim prim. Equivalent to UsdGeomBasisCurves::Get(prim.GetStage(), prim.GetPath()) for a valid prim , but will not immediately throw an error for an invalid prim.

inline explicit UsdGeomBasisCurves(const UsdSchemaBase &schemaObj)#: Construct a UsdGeomBasisCurves on the prim held by schemaObj . Should be preferred over UsdGeomBasisCurves(schemaObj.GetPrim()), as it preserves SchemaBase state.

inline virtual ~UsdGeomBasisCurves()#: Destructor.

inline UsdAttribute GetTypeAttr() const#

Linear curves interpolate linearly between two vertices. Cubic curves use a basis matrix with four vertices to interpolate a segment.


Declaration	`uniform token type = "cubic"`
C++ Type	TfToken
Usd Type	SdfValueTypeNames->Token
Variability	SdfVariabilityUniform
Allowed Values	linear, cubic

inline UsdAttribute CreateTypeAttr() const#: See GetTypeAttr(), and also Create vs Get Property Methods for when to use Get vs Create. If specified, author defaultValue as the attribute’s default, sparsely (when it makes sense to do so) if writeSparsely is true - the default for writeSparsely is false.

inline UsdAttribute GetBasisAttr() const#

The basis specifies the vstep and matrix used for cubic interpolation.


Declaration	`uniform token basis = "bezier"`
C++ Type	TfToken
Usd Type	SdfValueTypeNames->Token
Variability	SdfVariabilityUniform
Allowed Values	bezier, bspline, catmullRom

Note

The ‘hermite’ and ‘power’ tokens have been removed. We’ve provided UsdGeomHermiteCurves as an alternative for the ‘hermite’ basis.

inline UsdAttribute CreateBasisAttr() const#: See GetBasisAttr(), and also Create vs Get Property Methods for when to use Get vs Create. If specified, author defaultValue as the attribute’s default, sparsely (when it makes sense to do so) if writeSparsely is true - the default for writeSparsely is false.

inline UsdAttribute GetWrapAttr() const#

If wrap is set to periodic, the curve when rendered will repeat the initial vertices (dependent on the vstep) to close the curve. If wrap is set to ‘pinned’, phantom points may be created to ensure that the curve interpolation starts at P[0] and ends at P[n-1].


Declaration	`uniform token wrap = "nonperiodic"`
C++ Type	TfToken
Usd Type	SdfValueTypeNames->Token
Variability	SdfVariabilityUniform
Allowed Values	nonperiodic, periodic, pinned

inline UsdAttribute CreateWrapAttr() const#: See GetWrapAttr(), and also Create vs Get Property Methods for when to use Get vs Create. If specified, author defaultValue as the attribute’s default, sparsely (when it makes sense to do so) if writeSparsely is true - the default for writeSparsely is false.

inline UsdAttribute GetCurveVertexCountsAttr() const#

Curves-derived primitives can represent multiple distinct, potentially disconnected curves. The length of ‘curveVertexCounts’ gives the number of such curves, and each element describes the number of vertices in the corresponding curve.


Declaration	`int[] curveVertexCounts`
C++ Type	VtArray<int>
Usd Type	SdfValueTypeNames->IntArray

inline UsdAttribute CreateCurveVertexCountsAttr() const#: See GetCurveVertexCountsAttr(), and also Create vs Get Property Methods for when to use Get vs Create. If specified, author defaultValue as the attribute’s default, sparsely (when it makes sense to do so) if writeSparsely is true - the default for writeSparsely is false.

inline UsdAttribute GetWidthsAttr() const#

Provides width specification for the curves, whose application will depend on whether the curve is oriented (normals are defined for it), in which case widths are “ribbon width”, or unoriented, in which case widths are cylinder width. ‘widths’ is not a generic Primvar, but the number of elements in this attribute will be determined by its ‘interpolation’. See SetWidthsInterpolation() . If ‘widths’ and ‘primvars:widths’ are both specified, the latter has precedence.


Declaration	`float[] widths`
C++ Type	VtArray<float>
Usd Type	SdfValueTypeNames->FloatArray

inline UsdAttribute CreateWidthsAttr() const#: See GetWidthsAttr(), and also Create vs Get Property Methods for when to use Get vs Create. If specified, author defaultValue as the attribute’s default, sparsely (when it makes sense to do so) if writeSparsely is true - the default for writeSparsely is false.

inline UsdAttribute GetPointsAttr() const#

The primary geometry attribute for all PointBased primitives, describes points in (local) space.


Declaration	`point3f[] points`
C++ Type	VtArray<GfVec3f>
Usd Type	SdfValueTypeNames->Point3fArray

inline UsdAttribute CreatePointsAttr() const#: See GetPointsAttr(), and also Create vs Get Property Methods for when to use Get vs Create. If specified, author defaultValue as the attribute’s default, sparsely (when it makes sense to do so) if writeSparsely is true - the default for writeSparsely is false.

inline UsdAttribute GetVelocitiesAttr() const#

If provided, ‘velocities’ should be used by renderers to.

compute positions between samples for the ‘points’ attribute, rather than interpolating between neighboring ‘points’ samples. This is the only reasonable means of computing motion blur for topologically varying PointBased primitives. It follows that the length of each ‘velocities’ sample must match the length of the corresponding ‘points’ sample. Velocity is measured in position units per second, as per most simulation software. To convert to position units per UsdTimeCode, divide by UsdStage::GetTimeCodesPerSecond().

See also UsdGeom_VelocityInterpolation .


Declaration	`vector3f[] velocities`
C++ Type	VtArray<GfVec3f>
Usd Type	SdfValueTypeNames->Vector3fArray

inline UsdAttribute CreateVelocitiesAttr() const#: See GetVelocitiesAttr(), and also Create vs Get Property Methods for when to use Get vs Create. If specified, author defaultValue as the attribute’s default, sparsely (when it makes sense to do so) if writeSparsely is true - the default for writeSparsely is false.

inline UsdAttribute GetAccelerationsAttr() const#

If provided, ‘accelerations’ should be used with velocities to compute positions between samples for the ‘points’ attribute rather than interpolating between neighboring ‘points’ samples. Acceleration is measured in position units per second-squared. To convert to position units per squared UsdTimeCode, divide by the square of UsdStage::GetTimeCodesPerSecond().


Declaration	`vector3f[] accelerations`
C++ Type	VtArray<GfVec3f>
Usd Type	SdfValueTypeNames->Vector3fArray

inline UsdAttribute CreateAccelerationsAttr() const#: See GetAccelerationsAttr(), and also Create vs Get Property Methods for when to use Get vs Create. If specified, author defaultValue as the attribute’s default, sparsely (when it makes sense to do so) if writeSparsely is true - the default for writeSparsely is false.

inline UsdAttribute GetNormalsAttr() const#

Provide an object-space orientation for individual points, which, depending on subclass, may define a surface, curve, or free points. Note that ‘normals’ should not be authored on any Mesh that is subdivided, since the subdivision algorithm will define its own normals. ‘normals’ is not a generic primvar, but the number of elements in this attribute will be determined by its ‘interpolation’. See SetNormalsInterpolation() . If ‘normals’ and ‘primvars:normals’ are both specified, the latter has precedence.


Declaration	`normal3f[] normals`
C++ Type	VtArray<GfVec3f>
Usd Type	SdfValueTypeNames->Normal3fArray

inline UsdAttribute CreateNormalsAttr() const#: See GetNormalsAttr(), and also Create vs Get Property Methods for when to use Get vs Create. If specified, author defaultValue as the attribute’s default, sparsely (when it makes sense to do so) if writeSparsely is true - the default for writeSparsely is false.

inline UsdAttribute GetDisplayColorAttr() const#

It is useful to have an “official” colorSet that can be used as a display or modeling color, even in the absence of any specified shader for a gprim. DisplayColor serves this role; because it is a UsdGeomPrimvar, it can also be used as a gprim override for any shader that consumes a displayColor parameter.


Declaration	`color3f[] primvars:displayColor`
C++ Type	VtArray<GfVec3f>
Usd Type	SdfValueTypeNames->Color3fArray

inline UsdAttribute CreateDisplayColorAttr() const#: See GetDisplayColorAttr(), and also Create vs Get Property Methods for when to use Get vs Create. If specified, author defaultValue as the attribute’s default, sparsely (when it makes sense to do so) if writeSparsely is true - the default for writeSparsely is false.

inline UsdAttribute GetDisplayOpacityAttr() const#

Companion to displayColor that specifies opacity, broken out as an independent attribute rather than an rgba color, both so that each can be independently overridden, and because shaders rarely consume rgba parameters.


Declaration	`float[] primvars:displayOpacity`
C++ Type	VtArray<float>
Usd Type	SdfValueTypeNames->FloatArray

inline UsdAttribute CreateDisplayOpacityAttr() const#: See GetDisplayOpacityAttr(), and also Create vs Get Property Methods for when to use Get vs Create. If specified, author defaultValue as the attribute’s default, sparsely (when it makes sense to do so) if writeSparsely is true - the default for writeSparsely is false.

inline UsdAttribute GetDoubleSidedAttr() const#

Although some renderers treat all parametric or polygonal surfaces as if they were effectively laminae with outward-facing normals on both sides, some renderers derive significant optimizations by considering these surfaces to have only a single outward side, typically determined by control-point winding order and/or orientation. By doing so they can perform “backface culling” to avoid drawing the many polygons of most closed surfaces that face away from the viewer.

However, it is often advantageous to model thin objects such as paper and cloth as single, open surfaces that must be viewable from both sides, always. Setting a gprim’s doubleSided attribute to true instructs all renderers to disable optimizations such as backface culling for the gprim, and attempt (not all renderers are able to do so, but the USD reference GL renderer always will) to provide forward-facing normals on each side of the surface for lighting calculations.


Declaration	`uniform bool doubleSided = 0`
C++ Type	bool
Usd Type	SdfValueTypeNames->Bool
Variability	SdfVariabilityUniform

inline UsdAttribute CreateDoubleSidedAttr() const#: See GetDoubleSidedAttr(), and also Create vs Get Property Methods for when to use Get vs Create. If specified, author defaultValue as the attribute’s default, sparsely (when it makes sense to do so) if writeSparsely is true - the default for writeSparsely is false.

inline UsdAttribute GetOrientationAttr() const#

Orientation specifies whether the gprim’s surface normal should be computed using the right hand rule, or the left hand rule. Please see UsdGeom_WindingOrder for a deeper explanation and generalization of orientation to composed scenes with transformation hierarchies.


Declaration	`uniform token orientation = "rightHanded"`
C++ Type	TfToken
Usd Type	SdfValueTypeNames->Token
Variability	SdfVariabilityUniform
Allowed Values	rightHanded, leftHanded

inline UsdAttribute CreateOrientationAttr() const#: See GetOrientationAttr(), and also Create vs Get Property Methods for when to use Get vs Create. If specified, author defaultValue as the attribute’s default, sparsely (when it makes sense to do so) if writeSparsely is true - the default for writeSparsely is false.

inline UsdAttribute GetExtentAttr() const#

Extent is a three dimensional range measuring the geometric extent of the authored gprim in its own local space (i.e. its own transform not applied), without accounting for any shader-induced displacement. If any extent value has been authored for a given Boundable, then it should be authored at every timeSample at which geometry-affecting properties are authored, to ensure correct evaluation via ComputeExtent(). If no extent value has been authored, then ComputeExtent() will call the Boundable’s registered ComputeExtentFunction(), which may be expensive, which is why we strongly encourage proper authoring of extent.

An authored extent on a prim which has children is expected to include the extent of all children, as they will be pruned from BBox computation during traversal.

See also

ComputeExtent()

See also

Why Extent and not Bounds ?.


Declaration	`float3[] extent`
C++ Type	VtArray<GfVec3f>
Usd Type	SdfValueTypeNames->Float3Array

inline UsdAttribute CreateExtentAttr() const#: See GetExtentAttr(), and also Create vs Get Property Methods for when to use Get vs Create. If specified, author defaultValue as the attribute’s default, sparsely (when it makes sense to do so) if writeSparsely is true - the default for writeSparsely is false.

inline UsdAttribute GetXformOpOrderAttr() const#

Encodes the sequence of transformation operations in the order in which they should be pushed onto a transform stack while visiting a UsdStage’s prims in a graph traversal that will effect the desired positioning for this prim and its descendant prims.

You should rarely, if ever, need to manipulate this attribute directly. It is managed by the AddXformOp(), SetResetXformStack(), and SetXformOpOrder(), and consulted by GetOrderedXformOps() and GetLocalTransformation().


Declaration	`uniform token[] xformOpOrder`
C++ Type	VtArray<TfToken>
Usd Type	SdfValueTypeNames->TokenArray
Variability	SdfVariabilityUniform

inline UsdAttribute CreateXformOpOrderAttr() const#: See GetXformOpOrderAttr(), and also Create vs Get Property Methods for when to use Get vs Create. If specified, author defaultValue as the attribute’s default, sparsely (when it makes sense to do so) if writeSparsely is true - the default for writeSparsely is false.

inline UsdAttribute GetVisibilityAttr() const#

Visibility is meant to be the simplest form of “pruning” visibility that is supported by most DCC apps. Visibility is animatable, allowing a sub-tree of geometry to be present for some segment of a shot, and absent from others; unlike the action of deactivating geometry prims, invisible geometry is still available for inspection, for positioning, for defining volumes, etc.


Declaration	`token visibility = "inherited"`
C++ Type	TfToken
Usd Type	SdfValueTypeNames->Token
Allowed Values	inherited, invisible

inline UsdAttribute CreateVisibilityAttr() const#: See GetVisibilityAttr(), and also Create vs Get Property Methods for when to use Get vs Create. If specified, author defaultValue as the attribute’s default, sparsely (when it makes sense to do so) if writeSparsely is true - the default for writeSparsely is false.

inline UsdAttribute GetPurposeAttr() const#

Purpose is a classification of geometry into categories that can each be independently included or excluded from traversals of prims on a stage, such as rendering or bounding-box computation traversals.

See UsdGeom_ImageablePurpose for more detail about how purpose is computed and used.


Declaration	`uniform token purpose = "default"`
C++ Type	TfToken
Usd Type	SdfValueTypeNames->Token
Variability	SdfVariabilityUniform
Allowed Values	default, render, proxy, guide

inline UsdAttribute CreatePurposeAttr() const#: See GetPurposeAttr(), and also Create vs Get Property Methods for when to use Get vs Create. If specified, author defaultValue as the attribute’s default, sparsely (when it makes sense to do so) if writeSparsely is true - the default for writeSparsely is false.

inline UsdRelationship GetProxyPrimRel() const#

The proxyPrim relationship allows us to link a prim whose purpose is “render” to its (single target) purpose=”proxy” prim. This is entirely optional, but can be useful in several scenarios:

In a pipeline that does pruning (for complexity management) by deactivating prims composed from asset references, when we deactivate a purpose=”render” prim, we will be able to discover and additionally deactivate its associated purpose=”proxy” prim, so that preview renders reflect the pruning accurately.

DCC importers may be able to make more aggressive optimizations for interactive processing and display if they can discover the proxy for a given render prim.

With a little more work, a Hydra-based application will be able to map a picked proxy prim back to its render geometry for selection.

Note

It is only valid to author the proxyPrim relationship on prims whose purpose is “render”.

inline UsdRelationship CreateProxyPrimRel() const#: See GetProxyPrimRel(), and also Create vs Get Property Methods for when to use Get vs Create.

UsdPrim GetPrim() const#: Return this schema object’s held prim.

SdfPath GetPath() const#: Return the SdfPath to this schema object’s held prim.

inline explicit operator bool() const#

Check if this schema object is compatible with it’s held prim and that the prim is valid.

A typed schema object is compatible if the held prim’s type is or is a subtype of the schema’s type. Based on prim.IsA().

An API schema object is compatible if the API is of type SingleApplyAPI or UsdSchemaType::MultipleApplyAPI, and the schema has been applied to the prim. Based on prim.HasAPI.

This method invokes polymorphic behaviour.

See also

UsdSchemaBase::_IsCompatible()

Returns:: True if the help prim is valid, and the schema object is compatible with its held prim.

Public Static Functions

static inline UsdGeomBasisCurves Define( const UsdStageRefPtr &stage, const SdfPath &path, )#: Attempt to ensure a UsdPrim adhering to this schema at path is defined (according to UsdPrim::IsDefined()) on this stage.

Public Static Attributes

static const UsdSchemaType schemaType = UsdSchemaType::ConcreteTyped #

Compile time constant representing what kind of schema this class is.

See also

UsdSchemaType

Protected Functions

inline virtual bool _IsCompatible() const#

Helper for subclasses to do specific compatibility checking with the given prim. Subclassess may override _isCompatible to for example check type compatibility or value compatibility on the prim.

Overrides exist for UsdTyped and UsdAPISchemaBase.

This check is called when clients invoke the bool operator.

Returns:: True if the schema object is compatible with its held prim.

inline const TfToken _GetType() const#

Helper for subclasses to get this schema’s type token.

Note

This diverges from Usd and returns a TfToken, since we don’t implements TfType.

Returns:: The token representing the schema’s TfType.